前言
笔记来自百度架构师手把手带你零基础实践深度学习课程,第一天听下来,我感觉老师讲得还是非常深入浅出,通俗易懂的。推荐大家学一下。
课程链接:https://aistudio.baidu.com/aistudio/education/group/info/1297
虽然课程标题里说是零基础,但就和之前介绍过的零基础实现神经网络系列文章一样,这里的零基础指的是深度学习零基础。至少你要熟悉python编程,了解基本的数学原理(主要是线性代数和微积分),和部分库(比如Numpy)。博主在学习python和numpy的时候做了一点笔记,可以参考一下:
[post url="https://econ.wiki//wiki//编程语言//python//01 基础 Python笔记//" title="python基础语法" intro="雁陎做的关于python语法的笔记"]
[post url="https://econ.wiki//wiki//编程语言//python//02 numpy库//" title="numpy基础语法" intro="雁陎做的关于numpy语法的笔记"]
综述
人工智能、机器学习、深度学习的关系
概括来说,人工智能、机器学习和深度学习覆盖的技术范畴是逐层递减的。人工智能是最宽泛的概念。机器学习是当前比较有效的一种实现人工智能的方式。深度学习是机器学习算法中最热门的一个分支。如下图
机器学习
机器学习的实现
机器学习的实现可以分成两步:训练和预测,类似于我们熟悉的归纳和演绎。训练即从样本中抽样出输入和输出的关系,预测即给定新的输入,计算输出。
机器学习的方法论
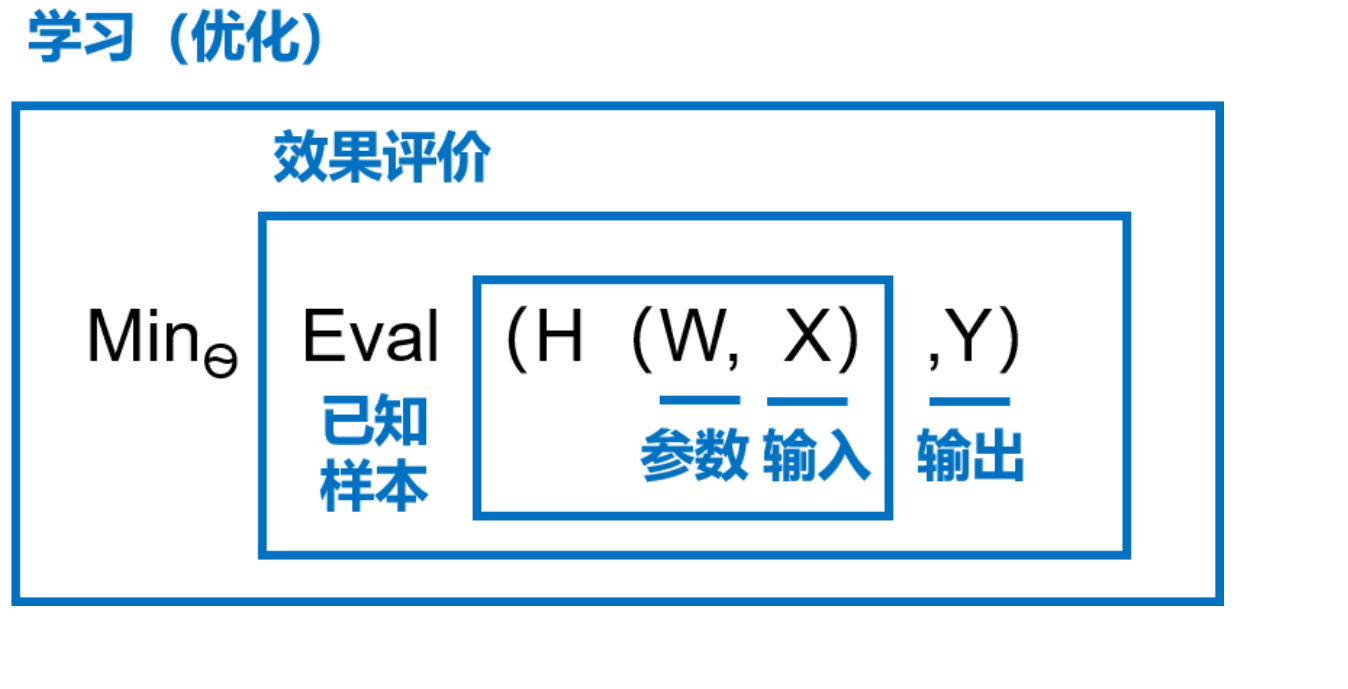
图3 是以$H$为模型的假设,它是一个关于参数$W$和输入$X$的函数,用$H(W, X)$ 表示。模型的优化目标是$H(W, X)$的输出与真实输出$Y$尽量一致,两者的相差程度即是模型效果的评价函数(相差越小越好)。那么,确定参数的过程就是在已知的样本上,不断减小该评价函数($H(W, X)$ 和$Y$相差)的过程,直到学习到一个参数$W$,使得评价函数的取值最小。这个衡量模型预测值和真实值差距的评价函数也被称为损失函数(损失Loss)。
最小化损失是模型的优化目标,实现损失最小化的方法称为优化算法,也称为寻解算法(找到使得损失函数最小的参数解)。参数$W$和输入$X$组成公式的基本结构称为假设。由此可见,模型假设、评价函数(损失/优化目标)和优化算法是构成模型的三个部分。
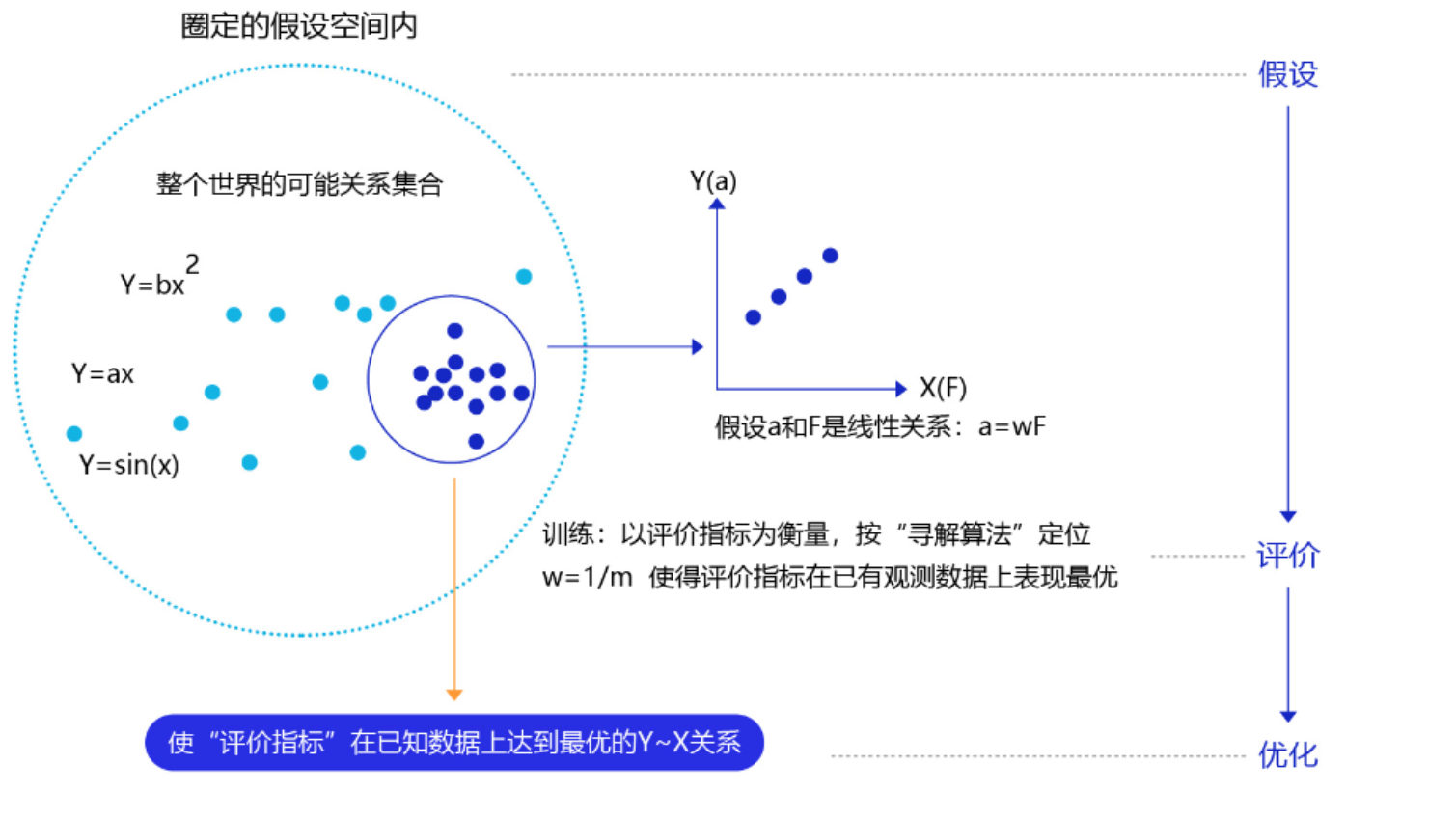
那么这三个部分是如何支撑机器学习流程的呢?如下图 所示:
- 模型假设:预先圈定好Y~X可能的关系(函数)集(篮圈),以提高训练效率。
- 评价函数:如何确定该函数就是我们要找的?定义一个评价函数,同样将拟合的误差最小作为优化目标。
- 优化算法:在关系可能性集中,寻找使得评价指标最优(损失函数最小/最拟合已有观测样本)的参数,这个寻找的方法即为优化算法。最笨的优化算法即按照参数的可能,穷举每一个可能取值来计算损失函数,保留使得损失函数最小的参数作为最终结果。
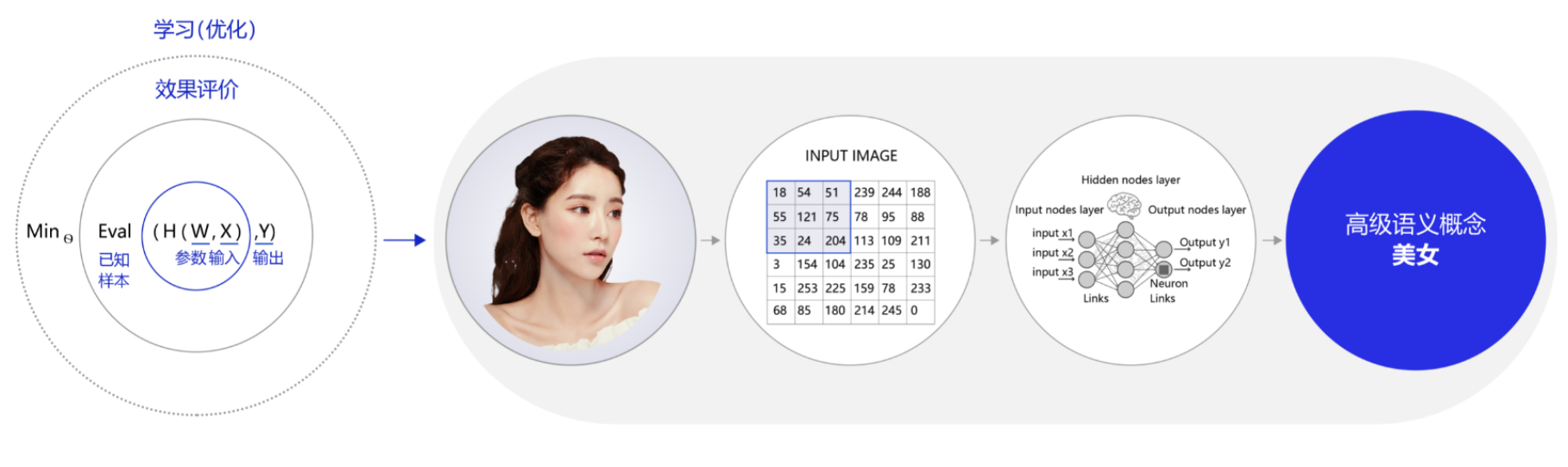
机器执行学习的框架体现了其学习的本质是“参数估计”(Learning is parameter estimation)。在此基础上,许多看起来完全不一样的问题都可以使用同样的框架进行学习,如科学定律、图像识别、机器翻译和自动问答等,它们的学习目标都是拟合一个“大公式”,如 图5 所示。
深度学习
深度学习与机器学习在理论结构上是一致的,即:模型假设、评价函数和优化算法,其根本差别在于假设的复杂度,如下图所示。
这种复杂程度已经无法单纯用数学公式表达,因此研究者设计了神经网络的模型。
神经网络
人工神经网络包括多个神经网络层,如卷积层、全连接层、LSTM等,每一层又包括很多神经元,超过三层的非线性神经网络都可以被称为深度神经网络。通俗的讲,深度学习的模型可以视为是输入到输出的映射函数,如图像到高级语义(美女)的映射,足够深的神经网络理论上可以拟合任何复杂的函数。因此神经网络非常适合学习样本数据的内在规律和表示层次,对文字、图像和语音任务有很好的适用性。因为这几个领域的任务是人工智能的基础模块,所以深度学习被称为实现人工智能的基础也就不足为奇了。
神经网络结构如 图7 所示。
一些基本概念:
神经元: 神经网络中每个节点称为神经元,由两部分组成:
- 加权和:将所有输入加权求和。
- 非线性变换(激活函数):加权和的结果经过一个非线性函数变换,让神经元计算具备非线性的能力。
- 多层连接: 大量这样的节点按照不同的层次排布,形成多层的结构连接起来,即称为神经网络。
- 前向计算: 从输入计算输出的过程,顺序从网络前至后。
- 计算图: 以图形化的方式展现神经网络的计算逻辑又称为计算图。我们也可以将神经网络的计算图以公式的方式表达如下:
$$Y =f_3 ( f_2 ( f_1 ( w_1\cdot x_1+w_2\cdot x_2+w_3\cdot x_3+b ) + … ) … ) … )$$
发展历程
- 1940年代:首次提出神经元的结构,但权重是不可学的。
- 1950-60年代:提出权重学习理论,神经元结构趋于完善,开启了神经网络的第一个黄金时代。
- 1969年:提出异或问题(人们惊奇的发现神经网络模型连简单的异或问题也无法解决,对其的期望从云端跌落到谷底),神经网络模型进入了被束之高阁的黑暗时代。
- 1986年:新提出的多层神经网络解决了异或问题,但随着90年代后理论更完备并且实践效果更好的SVM等机器学习模型的兴起,神经网络并未得到重视。
- 2010年左右:深度学习进入真正兴起时期。随着神经网络模型改进的技术在语音和计算机视觉任务上大放异彩,也逐渐被证明在更多的任务,如自然语言处理以及海量数据的任务上更加有效。至此,神经网络模型重新焕发生机,并有了一个更加响亮的名字:深度学习。
为何神经网络到2010年后才焕发生机呢?这与深度学习成功所依赖的先决条件:大数据涌现、硬件发展和算法优化有关。
影响
实现了端到端的学习
深度学习改变了很多领域算法的实现模式。在深度学习兴起之前,很多领域建模的思路是投入大量精力做特征工程,将专家对某个领域的“人工”理解沉淀成特征表达,然后使用简单模型完成任务(如分类或回归)。而在数据充足的情况下,深度学习模型可以实现端到端的学习,即不需要专门做特征工程,将原始的特征输入模型中,模型可同时完成特征提取和分类任务,如下图所示。
实现了深度学习框架标准化
- 从各算法均需独立实现到由统一的框架实现
- 从要求专业的理论储备与行业知识到只需少量的理论知识
基本流程
不同场景的深度学习模型具备一定的通用性,五个步骤即可完成模型的构建和训练,如下图所示
正是由于深度学习的建模和训练的过程存在通用性,在构建不同的模型时,只有模型三要素不同,其它步骤基本一致,深度学习框架才有用武之地。
案例:波士顿房价预测
波士顿房价预测是一个经典的机器学习任务,类似于程序员世界的“Hello World”。该数据集统计了13种可能影响房价的因素和该类型房屋的均价,期望构建一个基于13个因素进行房价预测的模型,如 图1 所示。
对于预测问题,可以根据预测输出的类型是连续的实数值,还是离散的标签,区分为回归任务和分类任务。因为房价是一个连续值,所以房价预测显然是一个回归任务。下面我们尝试用最简单的线性回归模型解决这个问题,并用神经网络来实现这个模型。
多元线性回归模型
假设房价和各影响因素之间能够用线性关系来描述:
$$y = {\sum_{j=1}^Mx_j w_j} + b$$
模型的求解即是通过数据拟合出每个$w_j$和$b$。其中,$w_j$和$b$分别表示该线性模型的权重和偏置。一维情况下,$w_j$ 和 $b$ 是直线的斜率和截距。
线性回归模型使用均方误差作为损失函数(Loss),用以衡量预测房价和真实房价的差异,公式如下:
$$MSE = \frac{1}{n} \sum_{i=1}^n(\hat{Y_i} - {Y_i})^{2}$$
第一步 数据处理
[scode type="yellow"]这部分代码原本是运行在jupyter上的,我搬过来的时候没有带运行结果,也省略了部分打印出来的语句[/scode]
读入数据
首先打开数据集看一下数据结构:
接着用numpy的fromfile函数读入数据
# 导入需要用到的package
import numpy as np
import json
# 读入训练数据
datafile = './work/housing.data'
data = np.fromfile(datafile, sep=' ')数据形状变换
由于读入的原始数据是1维的,所有数据都连在一起。因此需要我们将数据的形状进行变换,形成一个2维的矩阵,每行为一个数据样本(14个值),每个数据样本包含13个X(影响房价的特征)和一个Y(该类型房屋的均价)。
# 读入之后的数据被转化成1维array,其中array的第0-13项是第一条数据,第14-27项是第二条数据,以此类推....
# 这里对原始数据做reshape,变成N x 14的形式
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS',
'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
data = data.reshape([data.shape[0] // feature_num, feature_num])数据集划分
将数据集划分成训练集和测试集,其中训练集用于确定模型的参数,测试集用于评判模型的效果。为什么要对数据集进行拆分,而不能直接应用于模型训练呢?因为我们期望模型学习的是任务的本质规律,而不是训练数据本身,模型训练未使用的数据,才能更真实的评估模型的效果。
在本案例中,我们将80%的数据用作训练集,20%用作测试集,实现代码如下。通过打印训练集的形状,可以发现共有404个样本,每个样本含有13个特征和1个预测值。
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
training_data.shape数据归一化处理
对每个特征进行归一化处理(减平均值然后除以极差),使得每个特征的取值缩放到0~1之间。这样做有两个好处:一是模型训练更高效;二是特征前的权重大小可以代表该变量对预测结果的贡献度(因为每个特征值本身的范围相同)。
# 计算train数据集的最大值,最小值,平均值
maximums, minimums, avgs = \
training_data.max(axis=0), \
training_data.min(axis=0), \
training_data.sum(axis=0) / training_data.shape[0]
# 对数据进行归一化处理
for i in range(feature_num):
#print(maximums[i], minimums[i], avgs[i])
data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i])测试样本同样需要归一化,但需要注意的是,测试样本除以的也是训练样本的极差,为什么?因为我们测试的时候要尽可能拟合真实世界的情况,而真实世界里,我们一般拿不到样本的范围。
最后我们将其封装为一个函数load_data(),返回测试集和训练集,这里略。
第二步 模型设计-前向计算
神经网络的标准结构中每个神经元由加权和与非线性变换构成,然后将多个神经元分层的摆放并连接形成神经网络。线性回归模型可以认为是神经网络模型的一种极简特例,是一个只有加权和、没有非线性变换的神经元(无需形成网络),如下图所示:
神经网络的三个关键:加权和(留下),非线性变换(去掉),多层连接(去掉)
上图中的X = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ],Y = ['MEDV']
- 一层神经网络(一个神经元):$z=W \cdot x+b$
- 激活函数:$y=\text {activation}_{-} f n(z)$
- 对于线性回归activation_fn的形式:$y=z$
这个神经元就是将许多输入乘以一个线性的权重,进行加权和,之后再经过一个非线性的激活函数作为一个输出。该模型我们只用线性加权和的部分就足够了。
如果将输入特征和输出预测值均以向量表示,输入特征$x$有13个分量,$y$有1个分量,那么参数权重的形状(shape)是$13\times1$。假设我们以如下任意数字赋值参数做初始化:
$$w=[0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, -0.1, -0.2, -0.3, -0.4, 0.0]$$
w = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, -0.1, -0.2, -0.3, -0.4, 0.0]
w = np.array(w).reshape([13, 1])取出第1条样本数据,观察样本的特征向量与参数向量相乘的结果。
x1=x[0]
t = np.dot(x1, w)完整的线性回归公式,还需要初始化偏移量b,同样随意赋初值-0.2。那么,线性回归模型的完整输出是$z=t+b$,这个从特征和参数计算输出值的过程称为“前向计算”。
b = -0.2
z = t + b
将上述代码整合为一个类,forward函数(代表“前向计算”)完成上述从特征和参数到输出预测值的计算过程,代码如下所示。
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,
# 此处设置固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z调用它也很简单:
net = Network(13)
x1 = x[0]
y1 = y[0]
z = net.forward(x1)
print(z)如此,模型的基本框架就搭建好了。
第三步 损失函数
首先我们需要定义一个损失函数,来评估模型的有效性。回归模型中,通常采用均方误差来作为损失函数,公式如下:
$$Loss= \frac{1}{N}\sum_{i=1}^N{(y_i - z_i)^2}$$
其中,y是真实值,z是预测值,N为样本总数。
在Network类下面添加损失函数的计算过程如下:
class Network(object):
# ...
def loss(self, z, y):
error = z - y
cost = error * error
cost = np.mean(cost)
return cost计算Loss:
net = Network(13)
# 此处可以一次性计算多个样本的预测值和损失函数
x1 = x[0:3]
y1 = y[0:3]
z = net.forward(x1)
print('predict: ', z)
loss = net.loss(z, y1)
print('loss:', loss)第四步 优化算法
有损失函数是不够的,我们还需要找到一个方法,优化参数并使损失函数最小。也就是目标:找到一组参数(w,b)的值,使得Loss取极小值。
可以发现,Loss是以参数(w,b)为自变量的函数,回忆微分知识,易得,处于曲线极值点(这里是极小值)时的斜率为0,即函数在极值点处的导数为0
那么就好办了,我们只要求以下方程,将(x,y)代入即可
$$\frac{\partial{L}}{\partial{w}}=0$$
$$\frac{\partial{L}}{\partial{b}}=0$$
但是这种方法只对线性回归这样简单的任务有效。如果模型中含有非线性变换,或者损失函数不是均方差这种简单的形式,则很难通过上式求解。为了解决这个问题,下面我们将引入更加普适的数值求解方法:梯度下降法。
梯度下降法
想象一个山峰走到坡谷的盲人,他看不见坡谷在哪(无法逆向求解出$Loss$导数为0时的参数值),但可以伸脚探索身边的坡度(当前点的导数值,也称为梯度)。那么,求解Loss函数最小值可以这样实现:从当前的参数取值,一步步的按照下坡的方向下降,直到走到最低点。这种方法即“梯度下降法”。
训练的关键是找到一组$(w, b)$,使得损失函数$L$取极小值。我们先看一下损失函数$L$只随两个参数$w_5$、$w_9$变化时的简单情形,启发下寻解的思路。
$$L=L(w_5, w_9)$$
这里我们将$w_0, w_1, ..., w_{12}$中除$w_5, w_9$之外的参数和$b$都固定下来,可以用图画出$L(w_5, w_9)$的形式。
之所以挑这两个参数,主要是为了画图方便
net = Network(13)
losses = []
#只画出参数w5和w9在区间[-160, 160]的曲线部分,以及包含损失函数的极值
w5 = np.arange(-160.0, 160.0, 1.0)
w9 = np.arange(-160.0, 160.0, 1.0)
losses = np.zeros([len(w5), len(w9)])
#计算设定区域内每个参数取值所对应的Loss
for i in range(len(w5)):
for j in range(len(w9)):
net.w[5] = w5[i]
net.w[9] = w9[j]
z = net.forward(x)
loss = net.loss(z, y)
losses[i, j] = loss
#使用matplotlib将两个变量和对应的Loss作3D图
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = Axes3D(fig)
w5, w9 = np.meshgrid(w5, w9)
ax.plot_surface(w5, w9, losses, rstride=1, cstride=1, cmap='rainbow')
plt.show()对于这种简单情形,我们利用上面的程序,可以在三维空间中画出损失函数随参数变化的曲面图。从图中可以看出有些区域的函数值明显比周围的点小。
观察上述曲线呈现出“圆滑”的坡度,这正是我们选择以均方误差作为损失函数的原因之一。图6 呈现了只有一个参数维度时,均方误差和绝对值误差(只将每个样本的误差累加,不做平方处理)的损失函数曲线图。
由此可见,均方误差表现的“圆滑”的坡度有两个好处:
- 曲线的最低点是可导的。
- 越接近最低点,曲线的坡度逐渐放缓,有助于通过当前的梯度来判断接近最低点的程度(是否逐渐减少步长,以免错过最低点)。
而这两个特性绝对值误差是不具备的,这也是损失函数的设计不仅仅要考虑“合理性”,还要追求“易解性”的原因。
现在我们要找出一组$[w_5, w_9]$的值,使得损失函数最小,实现梯度下降法的方案如下:
- 步骤1:随机的选一组初始值,例如:$[w_5, w_9] = [-100.0, -100.0]$
- 步骤2:选取下一个点$[w_5^{'} , w_9^{'}]$,使得$L(w_5^{'} , w_9^{'}) < L(w_5, w_9)$
- 步骤3:重复步骤2,直到损失函数几乎不再下降。
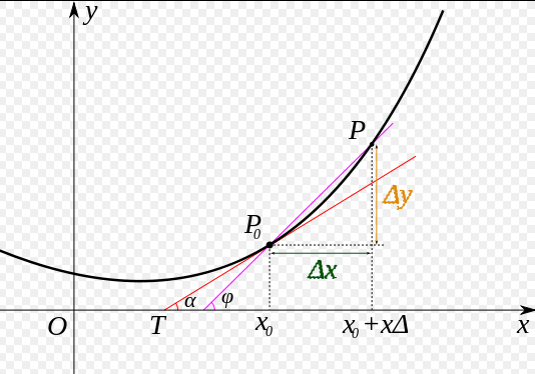
如何选择$[w_5^{'} , w_9^{'}]$是至关重要的,第一要保证$L$是下降的,第二要使得下降的趋势尽可能的快。微积分的基础知识告诉我们,沿着梯度的反方向,是函数值下降最快的方向,如 图7 所示。简单理解,函数在某一个点的梯度方向是曲线斜率最大的方向,但梯度方向是向上的,所以下降最快的是梯度的反方向。
计算梯度
上面我们讲过了损失函数的计算方法,这里稍微加以改写。为了梯度计算更加简洁,引入因子$\frac{1}{2}$,定义损失函数如下:
$$L= \frac{1}{2N}\sum_{i=1}^N{(y_i - z_i)^2}$$
其中$z_i$是网络对第$i$个样本的预测值:
$$z_i = \sum_{j=0}^{12}{x_i^{j}\cdot w_j} + b$$
梯度的定义:
$$gardient = (\frac{\partial{L}}{\partial{w_0}},\frac{\partial{L}}{\partial{w_1}}, ... ,\frac{\partial{L}}{\partial{w_{12}}} ,\frac{\partial{L}}{\partial{b}})$$
可以计算出$L$对$w$和$b$的偏导数:
$$\frac{\partial{L}}{\partial{w_j}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)\frac{\partial{z_i}}{\partial{w_j}}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)x_i^{j}}$$
$$\frac{\partial{L}}{\partial{b}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)\frac{\partial{z_i}}{\partial{b}}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)}$$
从导数的计算过程可以看出,因子$\frac{1}{2}$被消掉了,这是因为二次函数求导的时候会产生因子$2$,这也是我们将损失函数改写的原因。
下面我们考虑只有一个样本的情况下,计算梯度:
$$L= \frac{1}{2}{(y_i - z_i)^2}$$
$$z_1 = {x_1^{0}\cdot w_0} + {x_1^{1}\cdot w_1} + ... + {x_1^{12}\cdot w_{12}} + b$$
可以计算出:
$$L= \frac{1}{2}{({x_1^{0}\cdot w_0} + {x_1^{1}\cdot w_1} + ... + {x_1^{12}\cdot w_{12}} + b - y_1)^2}$$
可以计算出$L$对$w$和$b$的偏导数:
$$\frac{\partial{L}}{\partial{w_0}} = ({x_1^{0}\cdot w_0} + {x_1^{1}\cdot w_1} + ... + {x_1^{12}\cdot w_12} + b - y_1)\cdot x_1^{0}=({z_1} - {y_1})\cdot x_1^{0}$$
$$\frac{\partial{L}}{\partial{b}} = ({x_1^{0}\cdot w_0} + {x_1^{1}\cdot w_1} + ... + {x_1^{12}\cdot w_{12}} + b - y_1)\cdot 1 = ({z_1} - {y_1})$$
程序实现
首先,我们取出第一个样本:
x1 = x[0]
y1 = y[0]
z1 = net.forward(x1)然后求w0的梯度:
gradient_w0 = (z1 - y1) * x1[0]w1,w2……以此类推,写个for 循环即可求出所有w的梯度,再套个循环就能求出所有样本的所有w梯度。
Numpy实现梯度下降法
实际训练过程中,我们一般不会使用两层for这样低效的方法,而是借助Numpy的广播机制。计算梯度的代码中直接用$(z_1 - y_1) * x_1$,得到的是一个13维的向量,每个分量分别代表该维度的梯度。
x1 = x[0]
y1 = y[0]
z1 = net.forward(x1)
gradient_w = (z1 - y1) * x1
# 得出第一个样本的各维度梯度类似地,我们可以求样本2、样本3……的各个梯度,然后求平均值。
但是这仍然是种低效的做法,我们可以直接取出所有训练集样本作梯度运算,即:
z = net.forward(x)
gradient_w = (z - y) * x然后就会输出一个$13\times 404$维梯度矩阵(404是训练样本数量)。
上面gradient_w的每一行代表了一个样本对梯度的贡献。根据梯度的计算公式,总梯度是对每个样本对梯度贡献的平均值。
$$\frac{\partial{L}}{\partial{w_j}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)\frac{\partial{z_i}}{\partial{w_j}}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)x_i^{j}}$$
我们也可以使用Numpy的均值函数来完成此过程:
# axis = 0 表示把每一行做相加然后再除以总的行数
gradient_w = np.mean(gradient_w, axis=0)这里有个问题:gradient_w的形状是(13,)(我的理解是(1,13)),而w的维度是(13, 1)。导致该问题的原因是使用np.mean函数时消除了第0维。为了加减乘除等计算方便,gradient_w和w必须保持一致的形状。因此我们将gradient_w的维度也设置为(13, 1),代码如下:
gradient_w = gradient_w[:, np.newaxis]
# np.newaxis类似地,求b的梯度如下:
gradient_b = (z - y)
gradient_b = np.mean(gradient_b)
# 此处b是一个数值,所以可以直接用np.mean得到一个标量将上面计算w和b的梯度的过程,写成Network类的gradient函数,实现方法如下所示。
class Network(object):
# ...
def gradient(self, x, y):
z = self.forward(x)
gradient_w = (z-y)*x
gradient_w = np.mean(gradient_w, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = (z - y)
gradient_b = np.mean(gradient_b)
return gradient_w, gradient_b第五步 更新参数
下面我们开始研究更新梯度的方法。首先沿着梯度的反方向移动一小步,找到下一个点P1,观察损失函数的变化。
# 沿着梯度的反方向移动到下一个点P1
# 定义移动步长 eta
eta = 0.1
# 更新参数w
net.w = net.w - eta * gradient_w
# 重新计算z和loss
z = net.forward(x)
loss = net.loss(z, y)
gradient_w, gradient_b = net.gradient(x, y)
print('point {}, loss {}'.format(net.w, loss))
print('gradient {}'.format(gradient_w))在上述代码中,每次更新参数使用的语句:net.w = net.w - eta * gradient_w
- 相减:参数需要向梯度的反方向移动。
- eta:控制每次参数值沿着梯度反方向变动的大小,即每次移动的步长,又称为学习率。
这里我们可以回答之前留下的一个问题:为什么要进行归一化?
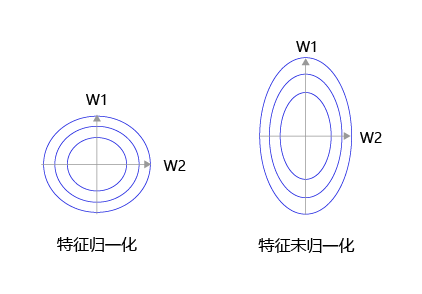
如 图8 所示,特征输入归一化后,不同参数输出的Loss是一个比较规整的曲线,学习率可以设置成统一的值 ;特征输入未归一化时,不同特征对应的参数所需的步长不一致,尺度较大的参数需要大步长,尺寸较小的参数需要小步长,导致无法设置统一的学习率。
代码整合与训练
我们将上面的循环计算封装为train()和update()函数,整个流程代码如下:
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
gradient_w = (z-y)*x
gradient_w = np.mean(gradient_w, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = (z - y)
gradient_b = np.mean(gradient_b)
return gradient_w, gradient_b
def update(self, gradient_w, gradient_b, eta = 0.01):
self.w = self.w - eta * gradient_w
self.b = self.b - eta * gradient_b
def train(self, x, y, iterations=100, eta=0.01):
losses = []
for i in range(iterations):
z = self.forward(x)
L = self.loss(z, y)
gradient_w, gradient_b = self.gradient(x, y)
self.update(gradient_w, gradient_b, eta)
losses.append(L)
if (i+1) % 10 == 0:
print('iter {}, loss {}'.format(i, L))
return losses
# 获取数据
train_data, test_data = load_data()
x = train_data[:, :-1]
y = train_data[:, -1:]
# 创建网络
net = Network(13)
num_iterations=1000
# 启动训练
losses = net.train(x,y, iterations=num_iterations, eta=0.01)
# 画出损失函数的变化趋势
plot_x = np.arange(num_iterations)
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()总结一下,梯度下降全流程如下:
- 通过前向计算拿到预测输出
- 根据预测值和实际值,计算损失
- 计算梯度
- 根据梯度更新参数
1-4循环往复,直到损失达到最小。
这样,一个简单的深度学习模型就搭建好了
修改:随机梯度下降法
在上述程序中,每次损失函数和梯度计算都是基于数据集中的全量数据。在实际问题中,数据集往往非常大,如果每次都使用全量数据进行计算,效率非常低。由于参数每次只沿着梯度反方向更新一点点,因此方向并不需要那么精确。一个合理的解决方案是每次从总的数据集中随机抽取出小部分数据来代表整体,基于这部分数据计算梯度和损失来更新参数,这种方法被称作随机梯度下降法(Stochastic Gradient Descent,SGD),核心概念如下:
- min-batch:每次迭代时抽取出来的一批数据被称为一个min-batch。(每次训练所需样本数据本身)
- batch_size:一个mini-batch所包含的样本数目称为batch_size。(每次训练所需样本数)
- epoch:当程序迭代的时候,按mini-batch逐渐抽取出样本,当把整个数据集都遍历到了的时候,则完成了一轮训练,也叫一个epoch。启动训练时,可以将训练的轮数num_epochs和batch_size作为参数传入。
下面结合程序介绍具体的实现过程,涉及到数据处理和训练过程两部分代码的修改。
数据处理修改
数据处理需要实现拆分数据批次和样本乱序(为了实现随机抽样的效果)两个功能。
通过大量实验发现,模型对最后出现的数据印象更加深刻。训练数据导入后,越接近模型训练结束,最后几个批次数据对模型参数的影响越大。为了避免模型记忆影响训练效果,需要进行样本乱序操作。
# 获取数据
train_data, test_data = load_data()
# 打乱样本顺序
np.random.shuffle(train_data)
# 将train_data分成多个mini_batch
batch_size = 10
n = len(train_data)
mini_batches = [train_data[k:k+batch_size] for k in range(0, n, batch_size)]
# 创建网络
net = Network(13)
# 依次使用每个mini_batch的数据进行训练
for mini_batch in mini_batches:
x = mini_batch[:, :-1]
y = mini_batch[:, -1:]
loss = net.train(x, y, iterations=1)训练过程代码修改
将每个随机抽取的mini-batch数据输入到模型中用于参数训练。训练过程的核心是两层循环:
1.第一层循环,代表样本集合要被训练遍历几次,称为“epoch”,代码如下:
for epoch_id in range(num_epoches):
2.第二层循环,代表每次遍历时,样本集合被拆分成的多个批次,需要全部执行训练,称为“iter (iteration)”,代码如下:
for iter_id,mini_batch in emumerate(mini_batches):
在两层循环的内部是经典的四步训练流程:前向计算->计算损失->计算梯度->更新参数,和前面是一样的。
修改后的代码如下:
import numpy as np
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
#np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
N = x.shape[0]
gradient_w = 1. / N * np.sum((z-y) * x, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = 1. / N * np.sum(z-y)
return gradient_w, gradient_b
def update(self, gradient_w, gradient_b, eta = 0.01):
self.w = self.w - eta * gradient_w
self.b = self.b - eta * gradient_b
def train(self, training_data, num_epoches, batch_size=10, eta=0.01):
n = len(training_data)
losses = []
for epoch_id in range(num_epoches):
# 在每轮迭代开始之前,将训练数据的顺序随机打乱
# 然后再按每次取batch_size条数据的方式取出
np.random.shuffle(training_data)
# 将训练数据进行拆分,每个mini_batch包含batch_size条的数据
mini_batches = [training_data[k:k+batch_size] for k in range(0, n, batch_size)]
for iter_id, mini_batch in enumerate(mini_batches):
#print(self.w.shape)
#print(self.b)
x = mini_batch[:, :-1]
y = mini_batch[:, -1:]
a = self.forward(x)
loss = self.loss(a, y)
gradient_w, gradient_b = self.gradient(x, y)
self.update(gradient_w, gradient_b, eta)
losses.append(loss)
print('Epoch {:3d} / iter {:3d}, loss = {:.4f}'.
format(epoch_id, iter_id, loss))
return losses
# 获取数据
train_data, test_data = load_data()
# 创建网络
net = Network(13)
# 启动训练
losses = net.train(train_data, num_epoches=50, batch_size=100, eta=0.1)
# 画出损失函数的变化趋势
plot_x = np.arange(len(losses))
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()版权属于:作者名称
本文链接:https://www.sitstars.com/archives/101/
转载时须注明出处及本声明